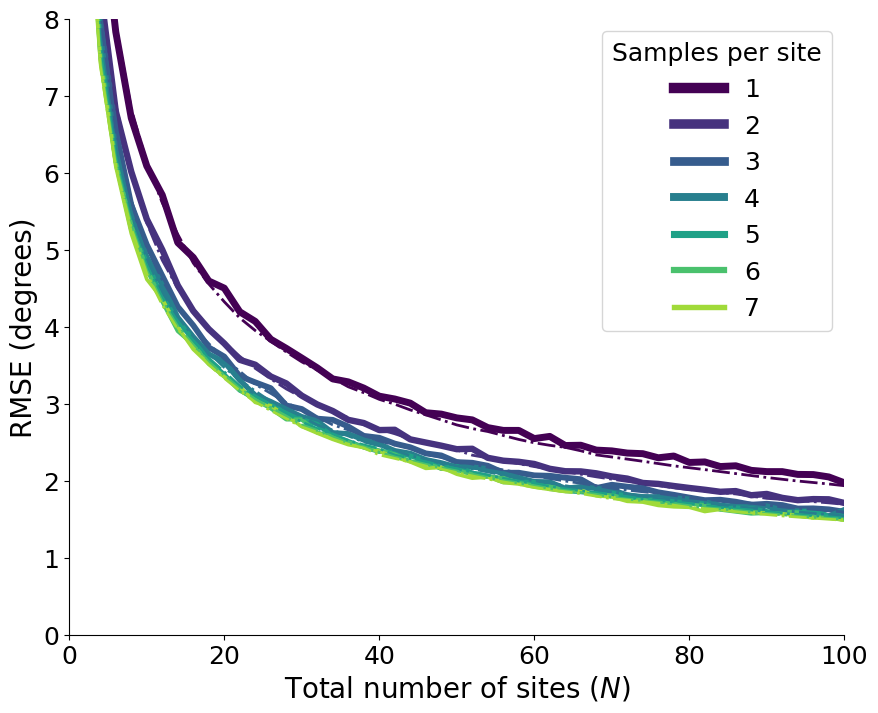
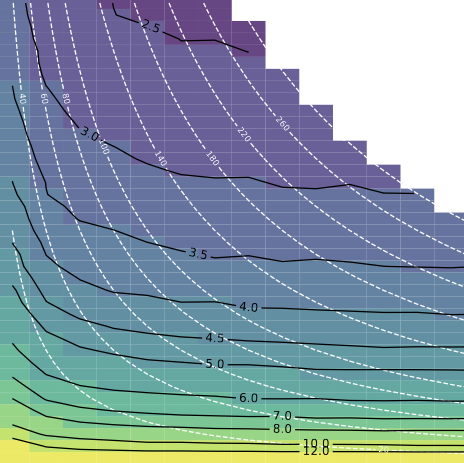
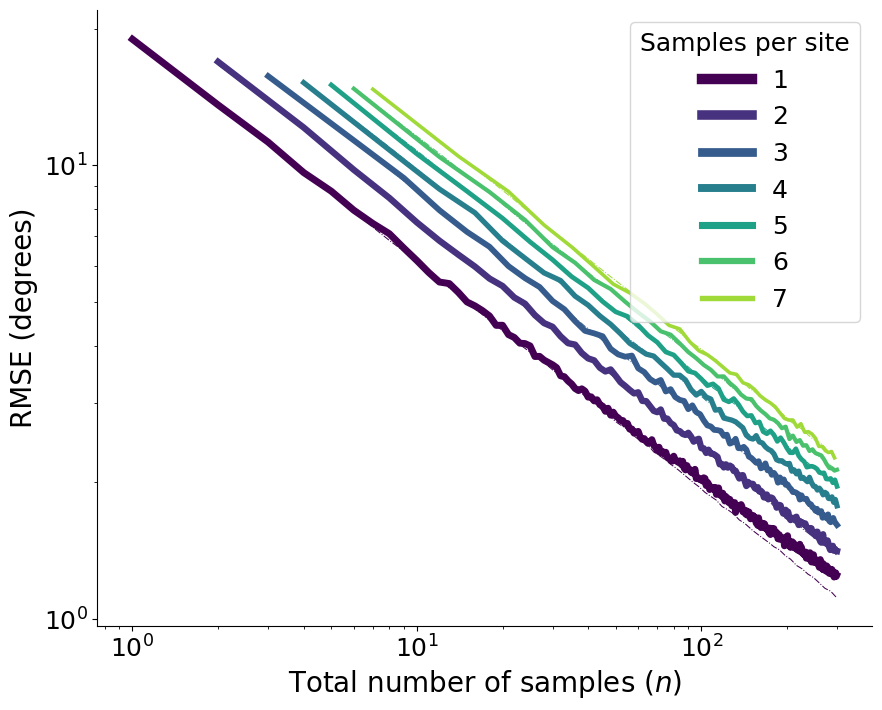
Figure 2: Decay as a function of the number of samples and sites

Contents

Figure 2: Decay as a function of the number of samples and sites#

These series of plots shows how the overall root mean squared error (RMSE) decays as we increase the number of totol samples and the number of sites for different choices of samples per site.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

import smpsite as smp

%matplotlib inline

1. Figures a & b: Decay as a function of the number of total samples \(n\)#

df = pd.read_csv('../../outputs/fig2ab_2000sim_summary.csv')
df

	Unnamed: 0	Unnamed: 1	error_angle_mean	error_angle_median	error_angle_25	error_angle_75	error_angle_95	error_angle_std	error_angle_S2	error_angle_S	...	N	n0	kappa_within_site	site_lat	site_long	outlier_rate	secular_method	kappa_secular	ignore_outliers	total_simulations
0	0	0	4.418425	4.068730	2.574621	5.931969	8.843983	2.389484	25.229262	5.022874	...	10	3	50	30.0	0.0	0.0	G	NaN	False	2000
1	1	0	3.564401	3.307917	2.101149	4.756044	7.050093	1.916513	16.376137	4.046744	...	24	1	50	30.0	0.0	0.0	G	NaN	False	2000
2	2	0	7.039044	6.605681	4.265727	9.247352	13.943720	3.726799	63.430232	7.964310	...	4	3	50	30.0	0.0	0.0	G	NaN	False	2000
3	3	0	1.238532	1.158910	0.764595	1.644945	2.368667	0.645502	1.950427	1.396577	...	229	1	50	30.0	0.0	0.0	G	NaN	False	2000
4	4	0	1.129028	1.053866	0.674889	1.512438	2.201005	0.590024	1.622659	1.273836	...	277	1	50	30.0	0.0	0.0	G	NaN	False	2000
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
771	771	0	1.534570	1.439038	0.929228	2.031131	2.954905	0.789545	2.977974	1.725681	...	87	3	50	30.0	0.0	0.0	G	NaN	False	2000
772	772	0	1.215589	1.158157	0.741750	1.638733	2.333324	0.615145	1.855872	1.362304	...	242	1	50	30.0	0.0	0.0	G	NaN	False	2000
773	773	0	2.524885	2.360240	1.513693	3.397144	4.986915	1.338083	8.164615	2.857379	...	35	2	50	30.0	0.0	0.0	G	NaN	False	2000
774	774	0	5.089531	4.711650	2.986586	6.697563	10.387042	2.796089	33.717527	5.806680	...	11	1	50	30.0	0.0	0.0	G	NaN	False	2000
775	775	0	1.662648	1.569897	1.007462	2.204899	3.196883	0.861498	3.506206	1.872487	...	117	1	50	30.0	0.0	0.0	G	NaN	False	2000

776 rows × 22 columns

df["error_kappa_theoretical"] = df.apply(lambda row: smp.kappa_theoretical(smp.Params(N=row.N, 
                                                                                      n0=row.n0, 
                                                                                      kappa_within_site=row.kappa_within_site,
                                                                                      site_lat=row.site_lat,
                                                                                      site_long=row.site_long, 
                                                                                      outlier_rate=row.outlier_rate, 
                                                                                      secular_method=row.secular_method, 
                                                                                      kappa_secular=row.kappa_secular)), axis=1)
df["error_angle_theoretical"] = df.apply(lambda row: float(smp.kappa2angular(row.error_kappa_theoretical)), axis=1)

fig, ax = plt.subplots(figsize=(10,8))

log_scale = True 

import matplotlib
palette = {x : matplotlib.cm.get_cmap('viridis')((x-1)/7) for x in np.arange(1,8)}

sizes = {i:5 - 0.4*(i-1) for i in range(1,8)}

sns.lineplot(ax=ax, data=df, x='n_tot', y='error_angle_S', hue='n0', size='n0', palette=palette, sizes=sizes)
sns.lineplot(ax=ax, data=df, x='n_tot', y='error_angle_theoretical', hue='n0', size=0.1, linewidth=2, palette=palette, legend=False, linestyle='dashdot')
# plt.xscale("log")

plt.xlabel("Total number of samples ($n$)", fontsize=20)
plt.ylabel("RMSE (degrees)", fontsize=20)
plt.yticks(fontsize=18)

leg = plt.legend(title="Samples per site", loc="upper right", fontsize=18, title_fontsize=18)
for i in range(7):
    leg.get_lines()[i].set_linewidth(1.5*sizes[i+1])
ax.spines[['right', 'top']].set_visible(False)

if log_scale:
    plt.xscale("log")
    plt.yscale("log")
    plt.xticks(fontsize=18)
    plt.savefig("Figure2b_log.pdf", format="pdf", bbox_inches='tight')
    plt.savefig("Figure2b_log.png", format="png", bbox_inches='tight')
else:
    plt.xticks([0, 50, 100, 150, 200, 250, 300], fontsize=18)
    plt.xlim(0, 300)
    plt.ylim(0, 8)
    plt.savefig("Figure2a.pdf", format="pdf", bbox_inches='tight')
    plt.savefig("Figure2a.png", format="png", bbox_inches='tight')

/tmp/ipykernel_2258/1007751571.py:6: MatplotlibDeprecationWarning: The get_cmap function was deprecated in Matplotlib 3.7 and will be removed two minor releases later. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap(obj)`` instead.
  palette = {x : matplotlib.cm.get_cmap('viridis')((x-1)/7) for x in np.arange(1,8)}

../../_images/af1fefcc00388d1586a52e91695d4504015dc5d1583ff52ef2f233bb80dd4978.png

df["error_kappa_theoretical"] = df.apply(lambda row: smp.kappa_theoretical(smp.Params(N=row.N, 
                                                                                      n0=row.n0, 
                                                                                      kappa_within_site=row.kappa_within_site,
                                                                                      site_lat=row.site_lat,
                                                                                      site_long=row.site_long,   
                                                                                      outlier_rate=row.outlier_rate, 
                                                                                      secular_method=row.secular_method, 
                                                                                      kappa_secular=row.kappa_secular)), axis=1)
df["error_angle_theoretical"] = df.apply(lambda row: float(smp.kappa2angular(row.error_kappa_theoretical)), axis=1)

Figure c & d: Decay as a function of the number of sites#

df = pd.read_csv('../../outputs/fig2cd_2000sim_summary.csv')
df

	Unnamed: 0	Unnamed: 1	error_angle_mean	error_angle_median	error_angle_25	error_angle_75	error_angle_95	error_angle_std	error_angle_S2	error_vgp_scatter	...	N	n0	kappa_within_site	site_lat	site_long	outlier_rate	secular_method	kappa_secular	ignore_outliers	total_simulations
0	0	0	3.507303	3.326483	2.133586	4.603671	6.762467	1.803921	15.553678	2.244988	...	14	6	50	30.0	0.0	0.0	G	NaN	False	2000
1	1	0	1.824976	1.716661	1.092270	2.457725	3.515834	0.944936	4.222996	1.319370	...	70	2	50	30.0	0.0	0.0	G	NaN	False	2000
2	2	0	2.755531	2.596467	1.664463	3.666091	5.281088	1.430537	9.638365	2.061391	...	30	2	50	30.0	0.0	0.0	G	NaN	False	2000
3	3	0	3.865201	3.690096	2.323372	5.129322	7.579034	2.014398	18.995552	2.327094	...	12	7	50	30.0	0.0	0.0	G	NaN	False	2000
4	4	0	2.231617	2.061765	1.363932	2.949242	4.350726	1.154125	6.311454	1.434520	...	36	5	50	30.0	0.0	0.0	G	NaN	False	2000
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
352	352	0	2.462295	2.297074	1.502908	3.300662	4.778267	1.280982	7.702988	1.632359	...	32	4	50	30.0	0.0	0.0	G	NaN	False	2000
353	353	0	1.979653	1.858608	1.168008	2.691842	3.864772	1.057756	5.037314	1.223433	...	44	7	50	30.0	0.0	0.0	G	NaN	False	2000
354	354	0	1.361468	1.278077	0.825126	1.807194	2.679220	0.722299	2.375049	0.878151	...	98	4	50	30.0	0.0	0.0	G	NaN	False	2000
355	355	0	2.096491	1.979148	1.295316	2.769094	4.051376	1.073121	5.546288	1.378519	...	46	3	50	30.0	0.0	0.0	G	NaN	False	2000
356	356	0	1.515558	1.421238	0.915071	2.030036	2.954767	0.801870	2.939590	0.954425	...	80	5	50	30.0	0.0	0.0	G	NaN	False	2000

357 rows × 21 columns

df["error_angle_S"] = df["error_angle_S2"] ** .5 

df["error_kappa_theoretical"] = df.apply(lambda row: smp.kappa_theoretical(smp.Params(N=row.N, 
                                                                                    n0=row.n0, 
                                                                                    kappa_within_site=row.kappa_within_site,
                                                                                    site_lat=row.site_lat,
                                                                                    site_long=row.site_long, 
                                                                                    outlier_rate=row.outlier_rate, 
                                                                                    secular_method=row.secular_method, 
                                                                                    kappa_secular=row.kappa_secular)), axis=1)
df["error_angle_theoretical"] = df.apply(lambda row: float(smp.kappa2angular(row.error_kappa_theoretical)), axis=1)

fig, ax = plt.subplots(figsize=(10,8))

log_scale = False
plot_theory = True

import matplotlib
palette = {x : matplotlib.cm.get_cmap('viridis')((x-1)/7) for x in np.arange(1,8)}

sizes = {i:5 - 0.4*(i-1) for i in range(1,8)}

sns.lineplot(ax=ax, data=df, x='N', y='error_angle_S', hue='n0', size='n0', palette=palette, sizes=sizes)
if plot_theory:
    sns.lineplot(ax=ax, data=df, x='N', y='error_angle_theoretical', hue='n0', linewidth=2, palette=palette, legend=False, linestyle='dashdot')


plt.xlabel("Total number of sites ($N$)", fontsize=20)
plt.ylabel("RMSE (degrees)", fontsize=20)
plt.yticks(fontsize=18)

leg = plt.legend(title="Samples per site", loc="upper right", fontsize=18, title_fontsize=18)
for i in range(7):
    leg.get_lines()[i].set_linewidth(1.5*sizes[i+1])
ax.spines[['right', 'top']].set_visible(False)

if log_scale:
    plt.xscale("log")
    plt.yscale("log")
    plt.xticks(fontsize=18)
    plt.savefig("Figure2d_log.pdf", format="pdf", bbox_inches='tight')
    plt.savefig("Figure2d_log.png", format="png", bbox_inches='tight')
else:
    plt.xticks(np.arange(0, 101, 20), fontsize=18)
    plt.xlim(0, 100)
    plt.ylim(0, 8)
    plt.savefig("Figure2c.pdf", format="pdf", bbox_inches='tight')
    plt.savefig("Figure2c.png", format="png", bbox_inches='tight')

/tmp/ipykernel_2258/3024017231.py:7: MatplotlibDeprecationWarning: The get_cmap function was deprecated in Matplotlib 3.7 and will be removed two minor releases later. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap(obj)`` instead.
  palette = {x : matplotlib.cm.get_cmap('viridis')((x-1)/7) for x in np.arange(1,8)}

../../_images/5ee0e8d54aaa30ef936d67993b2816f5fc8f31d27e4bbe9cb40771986df1f197.png